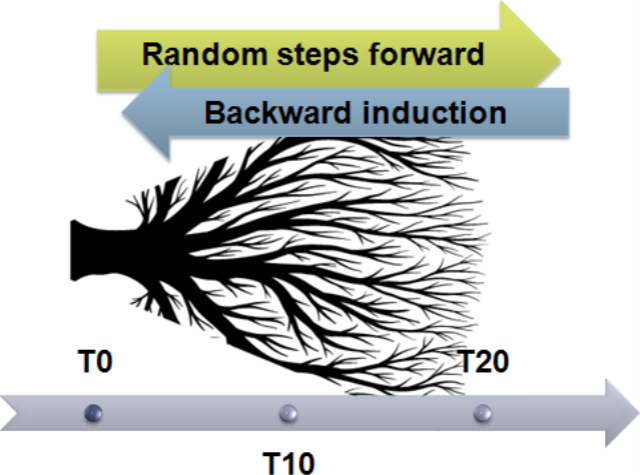
On the concentration properties of Interacting particle processes HAL-INRIA RR-7677 (2011),
Foundations and Trends in Machine Learning, Vol. 3, No. 3 - 4, 225-389 (2012). (online article, 167 pages)
| [ Main Page | Research | Publications | Management | Grants | Industrial contracts | Courses | Conferences | ALEA INRIA team | Collaborators | Other Application Areas ] |
 The software BIIPS is a general software developed by the INRIA team ALEA
for bayesian inference with interacting particle systems, a.k.a. Sequential Monte Carlo methods.
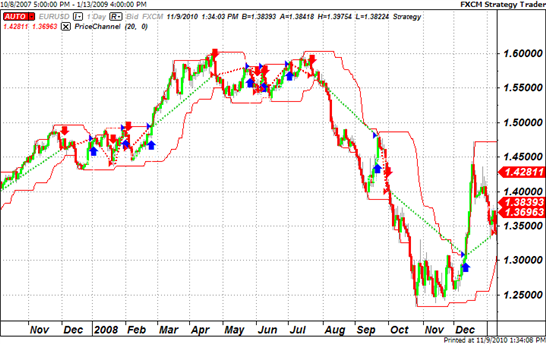
A demonstration of the BiiPS software for estimating the stochastic volatility of financial data can be found in
The software BIIPS is a general software developed by the INRIA team ALEA
for bayesian inference with interacting particle systems, a.k.a. Sequential Monte Carlo methods.
A demonstration of the BiiPS software for estimating the stochastic volatility of financial data can be found in