Feynman-Kac measures and Interacting Particle systems :

Selected studies on : Stochastic optimization, Regulation of processes, and Optimal control

---

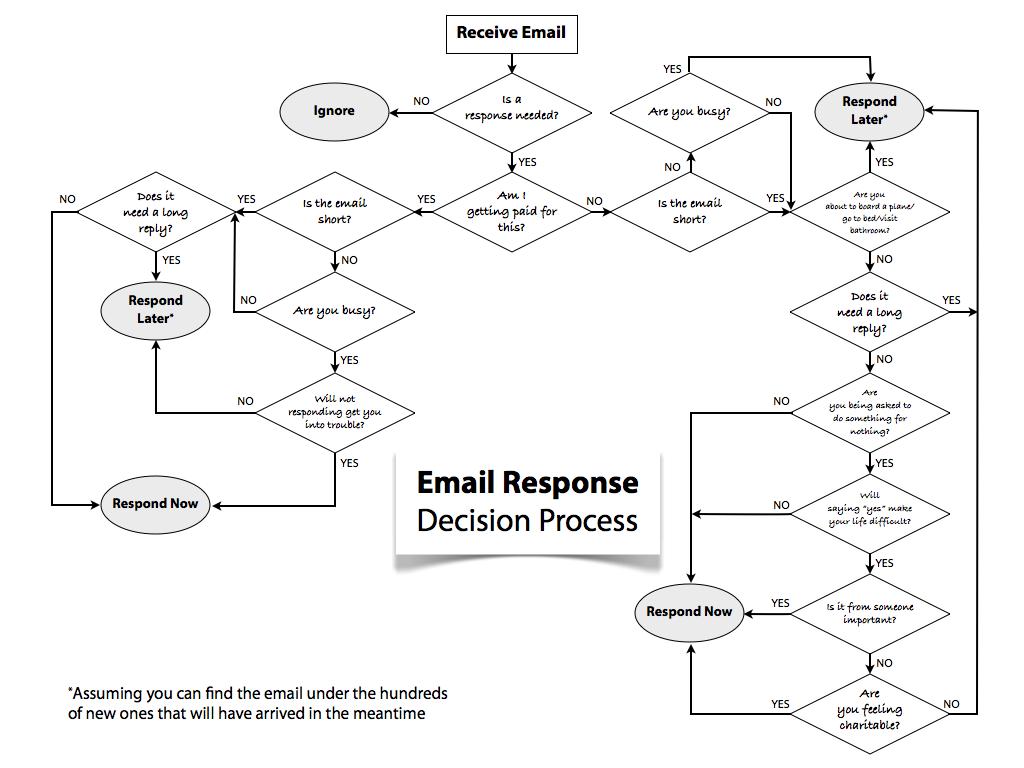
Software BiiPS


The software BIIPS is a general software developed by the INRIA team ALEA for bayesian inference with interacting particle systems, a.k.a. Sequential Monte Carlo methods. A demonstration of the BiiPS software for estimating the stochastic volatility of financial data can be found in


• BIIPS : Bayesian inference with interacting Particle Systems in Finance,
  



INRIA project manager : F. Caron, Design and developement engineer : A. Todeschini, Project contributors : P. Del Moral & P. Legrand, Logo designer : Timothée Del Moral.










---



• Projects homepages

  
  
  • Advanced Learning Evolutionary Algorithms (ALEA team project, Centre INRIA Bordeaux Sud-Ouest)
    
    
  • Sequential Monte Carlo Methods & Particle Filters Resources (Arnaud Doucet , Department of Statistics, Oxford University)
    
    
  • Applications of Interacting Particle Systems to Statistics (IRISA, INRIA Rennes)
    
    
  • Sequential Learning (SEQUEL project, INRIA Lille)
    
    
  • Sequential Monte Carlo homepage, particle filtering (Elena Punskaya , Department of Engineering, Cambridge University)
    
    
    
    
    
    
    
    
    
    
    
    

  ---

  
  
  

• Lectures presenting the particle methodology

  
  
  • Workshop on evolutionary algorithms. Challenges in theory and practice, 2010. [includes the link filtering<-->regulation]
    
  • CMAP Seminar in Polytechnique, 2011. [includes optimal stopping pb]
    
  • The ALEA Team project presentation in 2009. [includes the link filtering<-->regulation]
    
  • An introduction to particle methods in 2010 [includes the link filtering<-->regulation]
    
  
  More general lectures on the foundations and the applications of particle models
  
  
  • Sino-French Summer Institute 2011.Beijing, China, June 13-25, 2011. ((lecture note 1), (lecture note 2), and (lecture note 3))
    
  • INRIA Workshop on Statistical Learning Institut Henri Poincaré Paris, December 5-6, 2011 ( (lecture notes) )
  • University of Cambridge, Statistics Laboratory seminar, Feb. 2010. (lecture notes)
    
  • 10th Machine Learning summer school, September 1-15th, 2008. (lecture notes)
  • Opening workshop, Sequential Monte Carlo Methods, SAMSI, Duke Univ. September 7-10th, 2008. (lecture notes)
    
    
    
    
    
    
    
    

  ---

  
  
  

• Optimal Stopping times

  
  
  • P. Del Moral, P. Hu, N. Oudjane, Br. Rémillard. On the Robustness of the Snell envelope (HAL-INRIA RR-7303 2010) [35p].
    SIAM Journal on Financial Mathematics, vol.2, 587-626 (2011).
    
    
  • P. Del Moral, B. Rémillard, S. Rubenthaler. Monte Carlo approximations of american option that preserve monotonicity and convexity.
    Numerical Methods in Finance (28p.). Springer New York, Series : Proceeding in Mathematics, (to appear 2012).
    
    
  • P. Del Moral, P. Hu, and N. Oudjane. Snell Envelope with path dependent multiplicative optimality criteria, HAL-INRIA RR 7360 [18p] (2010).
    
    
  The forthcoming book on numerical methods in Finance also contains new developments on particle methods and their applications in optimal stopping time problems, including partially observed models :
  
  
  • Numerical Methods in Finance. R. Carmona, P. Del Moral, P. Hu, N. Oudjane. Springer New York, Series : Proceeding in Mathematics, (460p.) (to appear 2012).
  
  
  
  
  
  
  
  
  
  

  ---

  
  

• Maslov optimization theory

  
  
  • Maslov Optimization Theory: Optimality Versus Randomness.
    (P. Del Moral); Appendix of the book : Idempotency Analysis and its Applications, V.N. Kolokoltsov and V.P. Maslov, pages 243-302, Volume 401, Kluwer Academic Publishers, Dordrecht/Boston/London, Mathematics and its Applications (1997).
    
    
  • Maslov Optimization Theory : Stochastic Interpretation, Particle Resolution.
    (Del Moral P., Noyer J.C. and Salut G.); Proceedings XI Conf. Internationale sur l'analyse et l'optimisation des systèmes, Ecole des mines, Sophia Antipolis. Lecture Note in Control and Information Sciences 199. Springer-Verlag, 312-318 (1995).
    
    
  • Maslov idempotent probability calculus (Del Moral P., Doisy M.); Theor. Prob. Appl. vol. 43, No.4, 735 - 751 (1998) and vol. 44, No.2, 384 - 400 (1999).
    
    
  
  
  
  
  
  
  
  
  
  

  ---

  
  

• Decision genealogical trees and regulation of processes

  
  
  • Open-loop regulation and tracking control based on a genealogical decision tree. (K. Najim, E.Ikonen, and P.Del Moral; Neural Computing and Applications 15(3-4):339--349 (2006).)
    
    
  • Application of genealogical decision trees for open-loop tracking control (K. Najim, E.Ikonen, and P.Del Moral; Proceedings of the16th IFAC World Congress, Prague, Czech (2005).)
    
    
  • Sequential Monte Carlo methods for the optimization of a general class of objective functions (D. Crisan, P. Djuric, J. Miguez (2010).)
    
    
  • Sequential Monte Carlo Optimization Using Artificial State-Space Models (D. Crisan, P. Djuric, J. Miguez; Workshop and 5th IEEE Signal Processing (2009).)
    
    
  • Stochastic global optimization as a filtering problem (Panos Stinis Department of Mathematics University of Minnesota (2009).)
    
    
  
  
  
  

  ---

  

• Stochastic optimization

  
  
  • Global Estimation in Constrained Environments (Marin Kobilarov, Jerrold E. Marsden, Gaurav S. Sukhatme; Caletch (2009).)
    
    
  • Optimizing Over a Set of Manifolds (Juergen Gall, Angela Yao, and Luc Van Gool; Computer Vision Laboratory, ETH Zurich)
    
    
  • Stochastic design and control in random heterogeneous materials (Raphael Sternfels, Phaedon-Stelios Koutsourelakis, Cornell Univ. (2009).)
    
    
  • Interacting Particle Systems and Evolutionary Algorithms for Sparse Antenna Arrays (Alexandru-Adrian Tantar, Emilia Tantar, Pierre Del Moral, Pierre Minvielle, ALEA INRIA 2010)
    
    
  • Optimisation with SMC Samplers (Adam M. Johansen; Bridging the Gaps: Probabilistic Models for Optimisation 2007)
    
    
  • Random Search Algorithms (Zelda B. Zabinsky; Department of Industrial and Systems Engineering, University of Washington (2009).)
    
    
  • Online Multi-task Learning with Hard Constraints (Gabor Lugosi, Omiros Papaspiliopoulos, Gilles Stoltz (2009))
    
    
  • Investigations particulaires pour l'inférence statistique et l'optimisation de plans d'expériences (E. Parent, B. Amzal, Ph. Girard; J. Soc. Stat. France (2008))
    
    
  • Sequential Monte Carlo for Model Predictive Control (N. Kantas, A. Lecchini-Visintini, J.M. Maciejowski;Int. Workshop on Assessment and Future Directions of NMPC Pavia, 2008)
    
    
  • Simulation Based Bayesian Optimal Design of Aircraft Trajectories for Air Traffic Management (N. Kantas, A. Lecchini-Visintini, J.M. Maciejowski; Int. J. Adapt. Control Signal Process. (2010))
    
    

  ---

  
  
  
  
  

  Some Videos in YouTube on Genetic search algorithms

  
  
  

  Fish killer	Traveling Salesman Problem	Sounding the Stars	Adaptive robots	Architecture programming	Tower defense game	Tetris	Artificial Neural Network
  3D	Robotics	Drawing	Text Classification	Radiation Therapy	Human face	AI Flocking Evolution	Clustering
  Geronimo image	Green cloud computing	Evolving Truss Structuresg	GeneFlower robot	High Powered Particle Accelerators	Surface fluid wave lens	Antenna placement	Navigation algorithm

  
  
  
  
  
  
  
  
  

  ---

  
  
  

• Sequential Monte Carlo algorithms

  
  
  • Sequential Monte Carlo Samplers (Del Moral P., Doucet A., Jasra A) Journal of the Royal Society of Statistics, Series B. vol. 68, No. 3, pp. 411-436 (2006).
    
    
  • Particle Markov chain Monte Carlo methods (Ch. Andrieu, Arnaud Doucet, R. Holenstein , J. R. Statist. Soc. B (2010))
    
    
  • Branching and Interacting Particle Systems Approximations of Feynman-Kac Formulae with Applications to Non-Linear Filtering (Del Moral P., Miclo L.)
    Séminaire de Probabilités XXXIV, Ed. J. Azéma and M. Emery and M. Ledoux and M. Yor. Lecture Notes in Mathematics, Springer-Verlag Berlin, Vol. 1729, 1-145 (2000).
    
    
  • An Introduction to Interacting Simulated Annealing (Juergen Gall, Bodo Rosenhahn, and Hans-Peter Seidel, Max-Planck Institute for Computer Science)
    
    
  • The Gibbs Cloner for Combinatorial Optimization, Counting and Sampling (R. Rubinstein, Technion 2008)
    
    
  • Sequential Monte Carlo Simulated Annealing.(Enlu Zhou Xi Chen, Illinois Univ. 2011)
    
    
  • Sequentially Interacting Markov Chain Monte Carlo (A. Doucet, A.E. Brockwell; UBC and Carnegie Mellon Univ.)
    
    
  • On Adaptive Resampling Procedures for Sequential Monte Carlo Methods(Del Moral P., Doucet A., Jasra A) HAL-INRIA RR-6700 [46p], (Oct. 2008). To appear in Bernoulli (2011-2012).
    
    

  ---

  
  

• Recent tutorials & Surveys on Stochastic Particle Algorithms

  
  
  • Pierre Del Moral, Peng Hu, Liming Wu
    On the concentration properties of Interacting particle processes HAL-INRIA RR-7677 (2011),
    Foundations and Trends in Machine Learning, Vol. 3, No. 3 - 4, 225-389 (2012). (online article, 167 pages)
    
    
  • Particle Methods: An introduction with applications (Pierre Del Moral, Arnaud Doucet) HAL-INRIA RR-6991 [50p] (2009).
    2008 Machine Learning Summer School, Springer LNCS/LNAI Tutorial book no. 6368 (2010-2011).
    
    
  • Branching and Interacting Particle Systems Approximations of Feynman-Kac Formulae with Applications to Non-Linear Filtering
    (Del Moral P., Miclo L.) Séminaire de Probabilités XXXIV, Ed. J. Azéma and M. Emery and M. Ledoux and M. Yor.
    Lecture Notes in Mathematics, Springer-Verlag Berlin, Vol. 1729, 1-145 (2000).
    
    
  • A Mean Field Theory of Nonlinear Filtering (P. Del Moral, F. Patras, & S. Rubenthaler)
    the Oxford Handbook of Nonlinear Filtering, Oxford University Press, 2011)
    
    
  • An overview of existing methods and recent advances in sequential Monte Carlo (Olivier Cappe, Simon J. Godsill and Eric Moulines)
    
    
    
    
    
    
    
    

  ---