2016 RESULTS
Task 1 - Fast linear algebra solver in sparse linear solvers.
We continued the development of Strumpack fast linear solver and preconditioner library, which is based on hierarchical matrix algebra, e.g., Hierarchically Semi-Separable matrix (HSS) to obtain low-rank, data-sparse compression. The two significant achievements in 2016 are: 1) Finished and released the sparse version for distributed-memory (MPI+OpenMP). Its performance analysis paper was submitted to IPDPS2017. 2) Designed and implemented a novel adaptive sampling mechanism. Without this scheme, user must guess the numerical rank of the off-diagonal blocks, which is non-trivial for most problems. If the guess is too large, the code would use too many random vectors with decreased efficiency. If the guess is too small, the result would be inaccurate, then the user has to restart the process with a larger guess. Our adaptive scheme mitigate these problems by automatically incrementing the number of random vectors needed, while reusing the subspace information already computed before instead of restarting from the beginning each time. This greatly increased the efficiency, robustness and ease of use for Strumpack, both dense and sparse components. A paper is underway to evaluate the method and will be submitted to the PMAA special issue in Parallel Computing journal.
Combinatorial problems sparse symmetric linear solvers.
One such problem is reordering. In the case of symmetric matrices, one computes a permutation so that the symmetrically permuted matrix has a sparse factorization with a small amount of fill. We have continued to improve the robustness and efficiency of our implementations of the minimum local fill algorithm. In addition, we have successfully produced the first-ever distributed-memory implementation of the reverse Cuthill-McKee algorithm for reducing the profile of a sparse matrix. Our parallelization uses a two-dimensional sparse matrix decomposition. We achieve high performance by decomposing the problem into a small number of primitives and utilizing optimized implementations of these primitives. Our implementation shows strong scaling up to 1,024 cores for smaller matrices and up to 4,096 cores for larger matrices.
The notion of supernodes is important in sparse matrix factorization. Supernodes help to reduce indexing overhead and enable the use of dense matrix kernels. A related combinatorial problem is to reorder the columns within a supernode. Such a reordering will not affect the amount of fill in the factorization. It also will not change the number of floating-point operations. However, the local reordering, or reordering refinement, may help to enrich the sparsity structure within the supernodes so that the indexing overhead may be further reduced. More importantly, the reordering refinement may allow better use of dense matrix kernels. For example, it has been demonstrated by researchers at INRIA Bordeaux that the reordering refinement can help sparse matrix factorization on GPUs (see RR-8860 submitted to SIMAX). The researchers at INRIA Bordeaux have developed a very effective algorithm that is based on formulating the problem of finding such a reordering refinement as a Traveling Salesman Problem. We have developed an alternative reordering refinement heuristic, which appears to be effective and yet it is much less expensive than the algorithm based on the Traveling Salesman Problem.
Sparse Supernodal Solver using Low-Rank Compression We worked on the PaStiX sparse supernodal solver, using hierarchical compression to reduce the burden on large blocks appearing during the nested dissection process. We mainly focused on SVD and RRQR (Rank Revealing QR) as compression techniques right now.
Regarding a BLR (Block Low Rank) implementation, we have recently investigated two scenario:
Scenario BEGIN: Compress A
1. Compress large off-diagonal blocks in A (exploiting sparsity)
2. Eliminate each column block
2.1 Factorize the dense diagonal block
2.2 Apply a TRSM on LR blocks (cheaper) 2.3 LR update on LR matrices (extend-add)
3. Solve triangular systems with LR blocks
Scenario END: Compress L (similar to BLR-MUMPS: FCSU version)
1. Eliminate each column block
1.1 Factorize the dense diagonal block
1.2 Compress off-diagonal blocks belonging to the supernode
1.3 Apply a TRSM on LR blocks (cheaper)
1.4 LR update on dense matrices
2. Solve triangular systems with low-rank blocks
In terms of memory consumption, the BEGIN scenario saves memory, whereas the END scenario focuses on reducing the number of arithmetic operations, but supernodes are allocated in a dense fashion at the beginning (no gain in pure right-looking version).
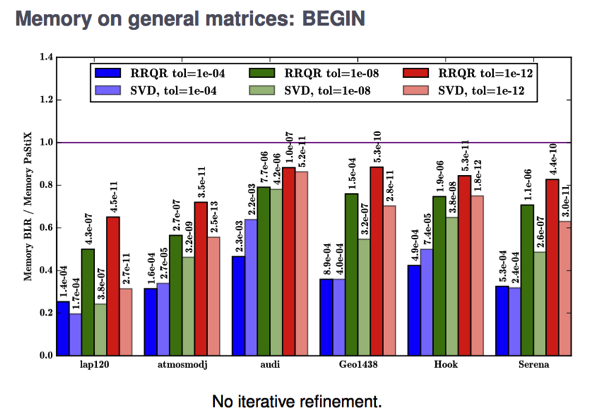 In terms of performances, the BEGIN scenario requires expensive extend-add algorithms to update (recompress) low-rank structures, whereas the END scenario continues to apply dense update at a smaller cost.
In terms of performances, the BEGIN scenario requires expensive extend-add algorithms to update (recompress) low-rank structures, whereas the END scenario continues to apply dense update at a smaller cost.
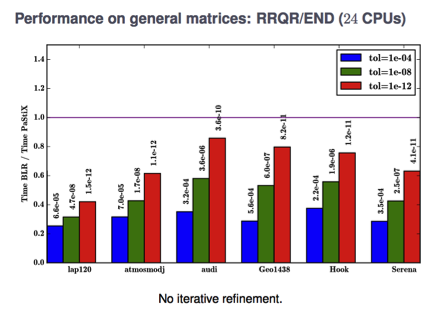
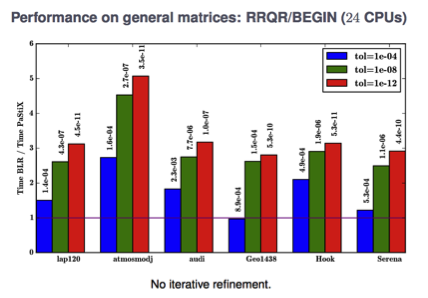
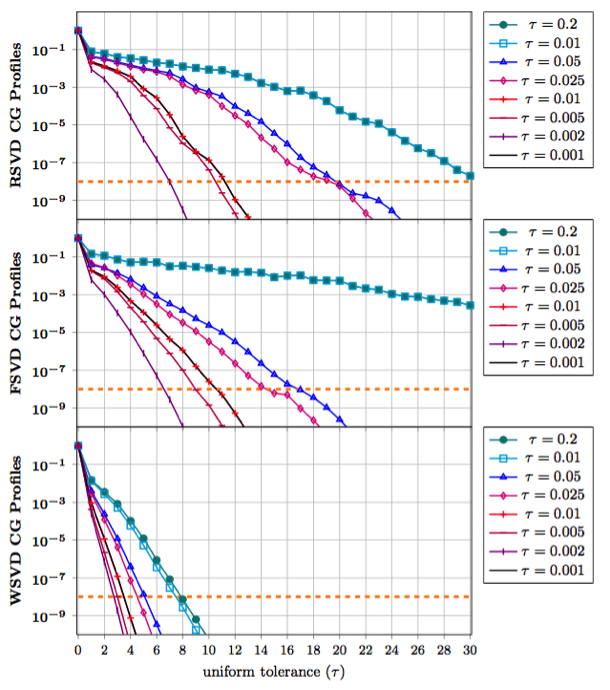 Figure: Convergence history for the solution of a diffusion equation, for three variants of data-sparse preconditioner when the threshold for the off diagonal block approximation is varied.
Figure: Convergence history for the solution of a diffusion equation, for three variants of data-sparse preconditioner when the threshold for the off diagonal block approximation is varied.
 In terms of performances, the BEGIN scenario requires expensive extend-add algorithms to update (recompress) low-rank structures, whereas the END scenario continues to apply dense update at a smaller cost.
In terms of performances, the BEGIN scenario requires expensive extend-add algorithms to update (recompress) low-rank structures, whereas the END scenario continues to apply dense update at a smaller cost.


To improve the efficiency of our sparse update kernel for both BLR (block low rank) and HODLR (hierarchically off-diagonal low-rank), we now investigate to BDLR (boundary distance low-rank) method to pre-select rows and columns in the low-rank approximation algorithm. We will also consider ordering strategies to enhance data locality and compressibility. On the condition number of preconditioning via HODLR compression for SPD matrices It seems natural to consider data sparse approximation for designing effective preconditioners for Krylov subspace methods. For symmetric positive definite (SPD) matrices, the condition number of the preconditioned matrix gives a tight indication on the capability of the preconditioner to speedup the convergence of the conjugate gradient method. In that framework, we develop an analysis to understand how computing the low rank approximation when using HODLR to build a data-sparse preconditioner. In particular, we have shown that our approach is optimal; that is, it minimizes the condition number when the rank of the off-diagonal blocks is given. Furthermore the analysis enables to clearly understand the spectral transformation induced by the low-rank approximation when compared to a more classical block diagonal preconditioner. Finally through numerical experiments, we illustrate the effectiveness of the new designed scheme (denoted WSVD for weighted SVD) that outperforms more classical techniques based on regular SVD (denoted RSVD) to approximate the off-diagonal blocks and SVD plus filtering (that enforces some directions such as the near null space of the matrix to be well captured by the preconditioner - denoted FSVD).
 Figure: Convergence history for the solution of a diffusion equation, for three variants of data-sparse preconditioner when the threshold for the off diagonal block approximation is varied.
Figure: Convergence history for the solution of a diffusion equation, for three variants of data-sparse preconditioner when the threshold for the off diagonal block approximation is varied.
Task 2 - Improved parallelism for modern computers for heterogeneous many-cores.
Recently we have been working on upgrading our sparse direct solver SuperLU to effectively utilize the many-core node architectures. We first focus on developing efficient "offload" strategies in order to use accelerators or co-processors, such as GPU or Intel Xeon Phi Knights Corners. A few months ago, we started porting SuperLU to the second generation Xeon Phi Knights Landing. For this, we have been restructuring the algorithm and code to expose more data parallelism in order to use long vector registers and high core count per node.
We have been designing and developing a new parallel direct solver for sparse symmetric systems of linear equations. Our solver, symPACK, is implemented for large-scale distributed-memory platforms. It employs several innovative ideas, including the use of an asynchronous task paradigm, one-sided communication, and dynamic scheduling. Our solver relies on efficient and flexible communication primitives provided by a UPC++ library. Preliminary performance evaluation has shown that symPACK demonstrates good scalability and that it is competitive when compared with state-of-the-art parallel distributed-memory symmetric factorization packages, validating our approach on practical cases.
Task 3 - Fast linear solvers for weak-hierarchical matrices
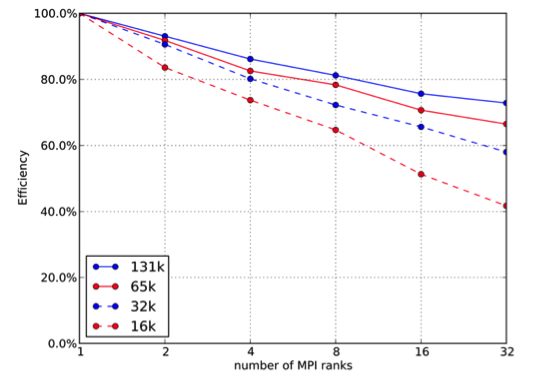
Solving sparse linear systems from the discretization of elliptic partial differential equations (PDEs) is an important building block in many engineering applications. Sparse direct solvers can solve general linear systems, but are usually slower and use much more memory than effective iterative solvers. To overcome these two disadvantages, a hierarchical solver (LoRaSp) based on H2-matrices was introduced in https://arxiv.org/abs/1510.07363. We have developed a parallel version of the algorithm in LoRaSp to solve large sparse matrices on distributed memory machines. The factorization time of our parallel solver scales almost linearly with the problem size for three-dimensional problems, as opposed to the quadratic scalability of many existing sparse direct solvers. Moreover, our solver leads to almost constant numbers of iterations when used as a preconditioner for Poisson problems. Our parallel algorithm also has significant speed-ups on more than one processor. As demonstrated by our numerical experiments, our parallel algorithm can solve large problems much faster than many existing packages.
The figure below shows a weak scaling of our parallel solver on a shared memory machine with 32 cores. The efficiency is shown on the y axis. The code was implemented using MPI.



 Menu
Menu See also
See also Contact
Contact