1-A FMM

Concerning the black-box method (bbFMM) different optimisations was developed to accelerate the operators involved in the far field computation. To do that, we exploit the tensor product form of the operators and the symmetries in the operators. This method have been implemented inside our ScalFMM code. A meticulous comparison between the Chebychev fast multipole method (bbFMM) and the classical method based on spherical expansion for 1/r kernel was realised.

1-B Hybrid

We have demonstrated that hybrid linear solvers provide a promising approach for solving difficult sparse linear systems arising from various applications. They are also natural in terms of implementations on today’s petascale, and future exascale, architectures. Currently, only a few groups worldwide are developing hybrid linear solvers. The FAST-LA project gives researchers at Berkeley Lab and INRIA an opportunity to collaborate and be at the forefront of an exciting research area.

We have initiated an intensive comparsion of the two hybrid iterative-direct approaches for the parallel solution of large sparse linear systems, namely MaPHyS for Inria at PDSLIN for LBNL. A set of test problems has been considered and experiments have been performed on both Inria (Plafrim) et LBNL/NERSC computing facilities. Further experiments deserved to be conducted to better understand the relative numerical robustness and parallel scalability of these two linear solvers.

We propose a new approach that achieves high performance across architectures. Our method consists of expressing the FMM algorithm as a task flow and employing a state-of-the-art runtime system, StarPU, in order to process the tasks on the different processing units.

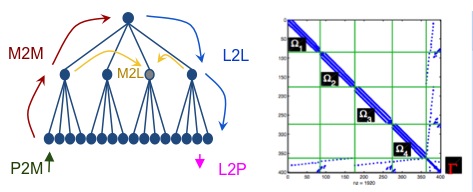
Many FMM algorithms are kernel specific, meaning, they require a distinct analytic treatment for each kernel function. Our approach can deal with a broad range of kernel functions based on Chebyshev interpolation. The interpolation polynomial is referred to as P2M (particle-to-moment), M2M (moment-to-moment), L2L (local-to- local) and L2P (local-to-particle) operator. The point-wise evaluated kernel function is referred as M2L (moment-to-local). The direct particle interactions are computed via the P2P (particle-to-particle) operator. The high-level algorithm can then be represented as a task graph (Figure below) where the nodes represent these operators.

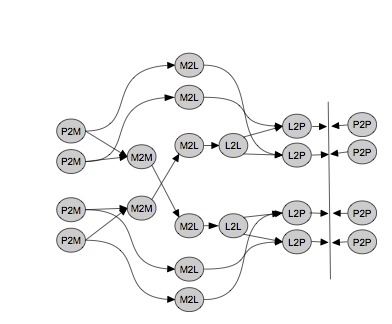
The P2P and M2L operators dominate the computational cost of the whole algorithm. Therefore, we have designed optimized versions of these kernels, which the runtime system can decide to execute on GPU.

The implementation of Chebychev kernels (P2P and M2L) was done in collobarotion with T. Takahashi (Department of Mechanical Science and Engineering, Nagoya University, Japan).

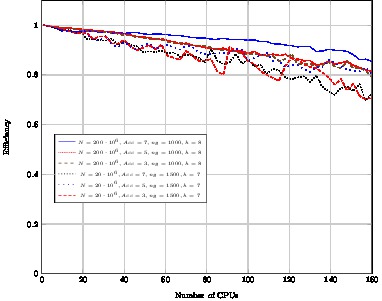
Homogeneous case

CPU Twenty octa-core Intel Xeon E7-8837 (160 CPUs)

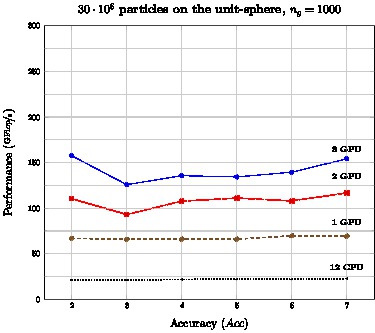
Heteregeneous

CPU: Dual-socket hexa-core Intel X5650 (12 CPU)

GPU NVidia M2090 Fermi accelerators (0 to 3 GPU)

These contributions will be presented during the poster session at SC'12 in Salt Lake City and in a minnisymposim at the SIAM conference on Comutational Sciences and Engineering (SCE13) in Boston. More details can be found in report RR-7981 (pdf).