In this project, we proposed to study fast and scalable hierarchical numerical kernels and their implementations on heterogeneous manycore platforms for two major computational kernels in intensive challenging applications. Namely, fast multipole methods (FMM) and sparse hybrid linear solvers, that appear in many intensive numerical simulations in computational sciences. The project was organized around two specific tasks to improve the algorithms/methods involved in the two computational kernels and a transversal one based on their implementation over a runtime system.

Fast Multipole Method Specific

Concerning the Chebyshev interpolation FMM method (bbFMM) developed at Stanford different optimisations (tensor product form and symmetries in the operators) was introduced to accelerate the operators involved in the far field computation. The method was also introduced in ScalFMM.

In order to allow larger Dislocation Dynamics (DD) simulations we focused on developing an efficient formulation of the isotropic elastic interaction forces between dislocations. We considered a tensorial interpolation scheme using both Chebyshev and uniform grid points and developed an efficient summation scheme suitable for fast multipole summation. The new algorithm based on this formulation is currently being implemented in the DD-code OptiDis, where the fast multipole summation is handled by ScalFMM library.

Direct/Hybrid Solver

Part of the Berkeley Lab team has been looking at the reordering problem for sparse Cholesky factorization. They showed that the problem of finding the best reordering to reduce fill-in is in general different from the problem of finding the best reordering to reduce work. They also showed that the latter problem is NP-complete. Motivated by this result, they re-examined the bottom-up reordering heuristics. In particular, they looked at the minimum local fill heuristic, which was believed to be very expensive and might not be much better than the well-known minimum degree heuristic. They demonstrated that efficient implementations of the minimum local fill heuristic exist and that the minimum local fill heuristic often produces better reorderings than the minimum degree heuristic, both in terms of fill and work.

Furthermore, we have been continuing to conduct a comparative study in term of performance and scalability between the two software packages developed at Berkeley Lab (PDSLIN) and Inria (MaPHyS). In particular, this had required some developments performed by S. Nakov (PhD in HiePACS) to enhance the robustness of the Inria solver by exploiting multi-level of parallelism; MPI plus threads on top of PaStiX. This comparative study will be part of the PhD manuscrit of S. Nakov that is expected to defend his PhD early 2015.

Sparse Direct Solver

We have been working on applying fast direct solvers for dense matrices to the solution of sparse direct systems. We are working with PaStiX. In parallel with this effort, we have developed a simpler multifrontal solver that can be used to benchmark our algorithms. During the benchmarks, we observed that the extend-add operation (during the sparse factorization) is the most time-consuming step. We have therefore developed a series of algorithms to reduce this computational cost. Specifically, the large dense matrices produced by the factorization (the frontal and update matrices for each node in the elimination tree) are replaced by HODLR (hierarchical off-diagonal low-rank, or strong-hierarchical) matrices. For this purpose, the boundary distance low-rank approximation scheme was used. The frontal matrix then looks like the following:

This structure was used to develop our fast solver. Here are two plots showing the reduction in CPU time and memory storage of the multifrontal sparse solver, as a result of using HODLR fast algebra:

The matrix size corresponds to the sparse matrix. At this point, the fast solver is used with a low-prescribed accuracy, and is currently coupled with an iterative scheme in order to produce the solution with near machine accuracy in only 10-15 iterations. Applying what we have learned about HODLR matrices, we are now working to incorporate them into the Inria code PaStiX. We have the ability to partition the supernodes in PaStiX. We are currently constructing the low-rank compressed structure of the supernodes using the BDLR algorithm mentioned above. Finally, the solvers discussed so far are limited in their efficiency by the assumption that all off-diagonal blocks are low-rank. In order to improve this, we are also developing fast solvers that use the more complicated weak-hierarchical structure (wH). With wH, the off-diagonal blocks are further subdivided into low-rank blocks and wH blocks. This structure is similar to the fast multipole method for example. With such a structure, we can ensure much higher accuracy with a lower rank. An efficient solver for wH matrices is currently under dewe observed that the extend-add operation (during the sparse factorization) is the most time-consuming step. We have therefore developed a series of algorithms to reduce this computational cost. Specifically, the large dense matrices produced by the factorization (the frontal and update matrices for each node in the elimination tree) are replaced by HODLR (hierarchical off-diagonal low-rank, or strong-hierarchical) matrices. For this purpose, the boundary distance low-rank approximation scheme was used. The frontal matrix then looks like the following: velopment. The algorithm is based on the extended sparsification idea (the graph of the extended sparse matrix for a 1D case after couple of eliminations is shown in the figure below). The hierarchical partitioning of the adjacency graph of the sparse matrix is done using the SCOTCH library. The well-separated fill-ins that appear during the elimination are recompressed, and presented as new interactions in the parent level. This is the main idea that makes the complexity of the overall algorithm linear.

Improved parallelism for modern computers for heterogeneous manycores

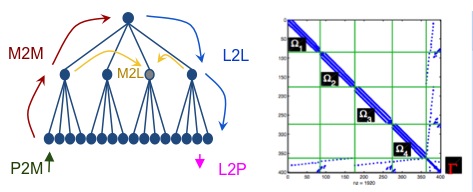
FMM - We proposed a new approach that achieves high performance across architectures. Our method consists of expressing the FMM algorithm as a task flow and employing a state-of-the-art runtime system, StarPU, in order to process the tasks on the different processing units. Many FMM algorithms are kernel specific, meaning, they require a distinct analytic treatment for each kernel function. Our approach can deal with a broad range of kernel functions based on Chebyshev interpolation. The interpolation polynomial is referred to as P2M (particle-to-moment), M2M (moment-to-moment), L2L (local-to- local) and L2P (local-to-particle) operator. The point-wise evaluated kernel function is referred as M2L (moment-to-local). The direct particle interactions are computed via the P2P (particle-to-particle) operator. The high-level algorithm can then be represented as a task graph where the nodes represent these operators A new parallel scheduler was developed for this purpose. We implemented a state-of-the-art OpenMP version of the code for benchmarking purposes. It was found that StarPU significantly outperforms OpenMP. Moreover we implemented the algorithm on top of heterogeneous machines (CPU+GPU) using StarPU. The FMM was also used to demonstrate the flexibility of StarPU for handling different types of processors. In particular we demonstrated in that application that StarPU can automatically select the appropriate version of a computational kernel (CPU or GPU version) and run it on the appropriate processor in order to minimize the overall runtime. Significant speed-up were obtained on heterogeneous platforms compared to multicore only processors.

We are working on a new parallel implementation of a sparse Cholesky factorization algorithm, as well as a parallel implementation of the minimum degree heuristic. The parallel sparse Cholesky factorization can be useful in dealing with subdomains in hybrid solvers. The parallel minimum degree heuristic and nested dissection heuristic (which is top-down strategy) can be combined to produce a hybrid reordering method.