Research Program

It is admitted today that numerical simulation is the third pillar for the development of scientific discovery at the same level as theory and experimentation. Numerous analyses also confirmed that high performance simulation will open new opportunities not only for research but also for a large spectrum of industrial sectors. On the route to exascale, emerging parallel platforms exhibit hierarchical structures both in their memory organization and in the granularity of the parallelism they can exploit. In this joint project between Inria HiePACS, Lawrence Berkeley National Laboratory (LBNL) and Stanford we propose to study, design and implement hierarchical parallel scalable numerical techniques to address two challenging numerical kernels involved in many intensive simulation codes: namely, N-body interaction calculations and the solution of large sparse linear systems. Those two kernels share common hierarchical features and algorithmic challenges as well as numerical tools such as low-rank matrix approximations expressed through H-matrix calculations. This project will address algorithmic and numerical challenges, and will result in parallel software prototype to be validated on large scale applications.

N-body simulations

In most scientific computing applications considered nowadays as computational challenges (like biological and material systems, astrophysics or electromagnetism), the introduction of hierarchical methods based on octree structures has dramatically reduced the amount of computation needed to simulate those systems for a given error tolerance. In N-body problems one computes all pair-wise interactions among N objects (particles, lines, etc.) at every time-step. The Fast Multipole Method (FMM) developed for gravitational potentials in astrophysics and for electrostatic (Coulombic) potentials in molecular simulations solves this N-body problem for any given precision with O(N) runtime complexity against O(N^2) for the direct computation. The potential field is decomposed in a near field part, which is directly computed, and a far field part approximated thanks to multipole and local expansions. The FMM has application in many other fields including elastic materials, Stokes’ flow, Helmholtz and Maxwell’s equations, the Laplace equation, etc. The main objective will be to design and to develop a generic high performance black-box or kernel-independent fast multipole method well suited for different application domains and with a good scalability on heterogeneous many-core platforms, including dealing with large irregular sets of objects. At this point, broadly speaking, two methods represent the current state of the art. First, fast O(N) methods exist for 1/|r| kernels. Since most kernels in material physics are defined in terms of derivatives of |r|. The disadvantage of these methods is that the algorithm is difficult to implement. In addition, choosing adequate parameters in the FMM to control the error and optimize the computational cost (order of expansion, size of leaf clusters, number of levels in the tree,... ) is challenging. Second, generic FMMs can be obtained by using Taylor expansions of kernels. This allows constructing low-rank approximation for any smooth function and requires only the calculation of the derivatives of the kernel. Again there are several drawbacks to this approach. The calculation of high order derivatives is difficult. Also, Taylor expansions are typically not optimal since they provide great accuracy near the center of the expansion but the error grows rapidly as the point r moves away from the center of the cluster. We propose to investigate the use of another class of method described in W. Fong and E. Darve, “The black-box fast multipole method,” J. Comp. Phys., 228 (23): pp. 8712-8725, 2009. This method offers several advantages including the fact that it is kernel independent; that is, the method can treat any smooth kernel without any additional analytical work or approximation formula, and it is optimal since it uses singular value decompositions (SVD) to obtain low-rank approximations. Also the pre-computation cost is negligible or small in most cases. The genericity, robustness and easy of use of the code that implements the O(N) methods will be validated in the framework of the challenging application that is dislocation dynamics.

Hybrid linear solvers

Solving large sparse linear systems Ax = b appears often in the inner-most loop of intensive simulation codes and is consequently the most time-consuming computation in many large-scale computer simulations in science and engineering, such as computational fluid dynamics, structural analysis, wave propagation, and design of new materials in nano-science, to name a few. There are two broad classes of approaches for solving linear systems of equations: sparse direct methods and iterative methods. Sparse direct solvers have been for years the methods of choice for solving linear systems of equations because of their reliable numerical behavior. However, it is nowadays admitted that such approaches are not scalable in terms of computational complexity or memory for large problems such as those arising from the discretization of large 3-dimensional partial differential equations (PDEs). Iterative methods, on the other hand, generate sequences of approximations to the solution. These methods have the advantage that the memory requirements are small. Also, they tend to be easier to be parallelized than direct methods. However, the main problem with this class of methods is the rate of convergence, which depends on the properties of the matrix. One way to improve the convergence rate is through preconditioning, which is another difficult problem. Our approach to high-performance, scalable solution of large sparse linear systems in parallel scientific computing is to combine direct and iterative methods. Such a hybrid approach exploits the advantages of both direct and iterative methods. The iterative component allows us to use a small amount of memory and provides a natural way for parallelization. The direct part provides its favorable numerical properties with finer levels of parallelism. 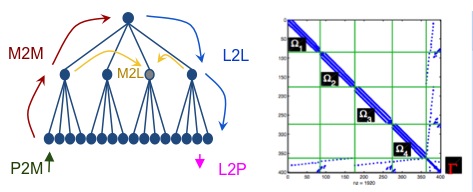The approaches followed by the teams involved in this proposal rely on non-overlapping techniques that require the exact factorization of small (sub-domains) problems enabling the solution of the so-called Schur complement system. H-matrices are a special class of matrices, which essentially are such that certain off diagonal blocks can be well approximated using low-rank matrices. The theory has been developed so far in the context of dense matrices (the natural setting for H-matrices). The FMM is based on a special type of H-matrix (sometimes called H2 matrix). It has been shown that direct solvers with computational cost in O(N) can be constructed for H-matrices of size N. Such matrices also appear in hybrid solvers, in form of the Schur complement for the sub-domains. In addition, direct solvers applied to sparse matrices lead to dense frontal blocks which themselves have an H-matrix structure. We will therefore be able to apply fast methods arising from the field of H-matrices at many levels: as part of the direct solvers for the sub-domains, and to accelerate the formation and application of the Schur complement operators. It could also be applied in certain parts of the iterative solvers, for example to form preconditioners. Many exciting avenues of research are therefore possible, which we will explore. The parallel implementations of the FMM and hybrid solvers are targeted at heterogeneous many-core node parallel platforms. In order to enhance the portability and the flexibility of use, we will use run-time systems, such as StarPU or DAGUE currently used in the ongoing associate team MORSE, with the University of Tennessee at Knoxville and the University of Colorado at Denver, for our software realization.