Research program

 

It is organized in 4 tasks as follow

task 1: Comparison and analysis of the current numerical schemes under study by the three partners.

1-A: FMM: this task will focus on comparing different FMM formulations and their efficiency and ease of use in the context of electrostatic/astrophysics and dislocation kernels. The goal is to choose a robust, versatile, and efficient method. (Inria, Stanford)

1-B: Hybrid solvers: (INRIA, LBNL)

• Complement the comparison study initiated during the FBF by addressing classes of problems not yet considered (augmented systems, fully unsymmetric) and use as much as possible common building boxes (e.g. local sparse direct solvers).
• Analyse the possible trade-offs between the different approaches

1-C: Synthesis in the view of forthcoming heterogeneous many-core implementations. (All)

Task 2: FMM specific

2-A: Adapt for isotropic dislocation kernels. This will require extending the formalism for 1/r to dislocation kernels. This will be compared with the black box FMM of Fong. The goal is to assess the ease of implementation, robustness, performance, and accuracy. (INRIA, Stanford)

2-B: Analysis of the benefit and impact on the algorithm design of the low rank approximation techniques. We will compare the use of the SVD with adaptive cross approximations (ACA). Even though ACA is not optimal like SVD, that is the rank obtained with ACA for a target accuracy is typically somewhat larger than with the SVD, the pre-computational cost is significantly smaller than SVD. (INRIA, Stanford)

2-C: Design improvement of the methods for parallel computers and many-core processors. We will consider for example the combination of FMM and tree methods. The latter have more flops and also more parallel instructions. A combination of both approaches may prove more efficient than each method taken separately. (INRIA, Stanford) 2-D: Validation on large scale challenging dislocation problems from the two partners. (INRIA, Stanford)

Task 3: Hybrid specific

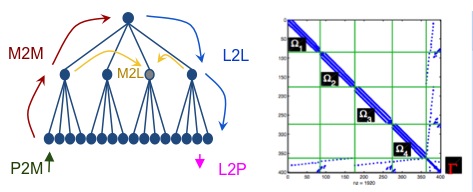
3-A: Design new preconditioning techniques whose features results from the analysis conducted in task 1-B. (INRIA, LBNL)

3-B: Study the use of low rank techniques (H-matrix, HSS matrices) to design fast direct solvers able to compute approximation of Schur complements. This research task will be developed in close relationship with the effort conduced in task 2-B. This task requires several sub-tasks and will represent a significant effort. (All)

3-C: Validation on large scale challenging problems from the three partners. (All)

Task 4: Improved parallelism for modern computers for heterogeneous manycores

4-A: Improvement of the parallel performance and scalability using hybrid parallelism (e.g. MPI+OpenMP+CUDA). (All)

4-B: A more prospective approach is to consider DAG formalism and runtime system to schedule tasks. As the computers are more and more complex (hierarchical memory, accelerators, large number of cores), a new paradigm based on a DAG (directed acyclic graph) of tasks will be applied. This allows analysing the dependency between the parallel tasks to generate an optimal execution schedule by a runtime framework like StarPU. This will be very useful to coordinate the work between the GPU and the multi-core processors. Case studies will include the FMM and the hybrid solvers. (All)