




Next: Fit parameters
Up: Detailed description of program
Previous: Spectrum parameters
Contents
Index
The GMRES method is used to solve the following linear system for the polarisability, 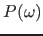 ,
,
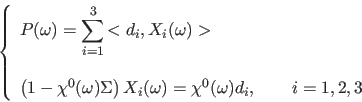 |
(2) |
where 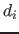 is the dipole in the
is the dipole in the 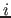 -direction,
-direction, 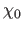 is the susceptibility of the non-interacting Kohn-Sham system and
is the susceptibility of the non-interacting Kohn-Sham system and 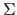 the interaction kernel, cf. papers 1-3. The parameters of the method are:
the interaction kernel, cf. papers 1-3. The parameters of the method are:
- solver_krylov
- (integer): Maximum dimension of the Krylov space. This parameter is also called the restart parameter and it controls the amount of memory required by the matrix in the Krylov space.
Default: 20
- solver_itermax
- (integer): Maximum number of iterations to reach convergence.
Default: 100
- solver_verbose
- (integer): Controls output of information on convergence of the solver. If the value is non-zero, output is written in file fort.solver_verbose.
Default: 0
- solver_eps
- (real): tolerance for convergence.
Default: 0.001
Olivier Coulaud
2013-11-09
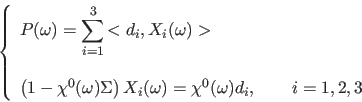
![]() is the dipole in the
is the dipole in the ![]() -direction,
-direction, ![]() is the susceptibility of the non-interacting Kohn-Sham system and
is the susceptibility of the non-interacting Kohn-Sham system and ![]() the interaction kernel, cf. papers 1-3. The parameters of the method are:
the interaction kernel, cf. papers 1-3. The parameters of the method are: